Missing data can be a common issue. Data scientists have to deal with this before they can send their data through a traditional machine learning system. Using a process called imputation, the data scientist can fill in missing values in their dataset. But there are lots questions that come up in the process. Among them:
- If an observation contains a missing value for one or more features, should the observation be discarded?
- If the same feature is frequently missing (e.g. say people skip the "income bracket" question), should the feature be dropped from the dataset?
- What if this feature is highly informative when the data is populated? Wouldn't it be nice to include the feature when it is present.
- Which imputation strategy should be used? Can/should multiple strategies be used?
- Doesn't data imputation introduce bias into the system? Can this be minimized?
Imputation adds a level of complexity on top of an already complex machine learning system. Even after choosing an imputation strategy, the data scientist may continue to second-guess whether the chosen strategy is sufficient. It would be incredibly convenient if a machine learning system could just operate on a dataset that has missing values.
The NIML system does not require data imputation.
The challenges for this week focus on exploring how NIML (and perhaps other systems) handle missing data:
- Modify your own dataset by injecting missing values and see how NIML responds
- Take a dataset with missing values and impute. Compare/contrast how NIML behaves on the missing-value dataset verses the imputed dataset
- Take a missing-values dataset and run it through NIML and also through another ML system and compare/contrast the results from the two systems
We challenge you to take the concepts here and apply them to a dataset of your choosing, and then explore beyond that!
Step 1 - DataFirst, we need to load in the dataset (we will use scikit-learn's wine dataset) and convert it into a form appropriate for NIML.
from sklearn import datasets from sklearn.model_selection import train_test_split import random random.seed(9411) # for repeatable results data_file = datasets.load_wine() niml_data = [] for idx in range(len(data_file.data)): row = [str(data_file.target[idx])] # column 0 = target label row.extend(data_file.data[idx]) # all other columns = feature values niml_data.append(row) random.shuffle(niml_data)
What does missing data look like in NIML?
Let's briefly look at what NIML does when data is missing. In last week's challenge, we used a function to plot encoded data. We will use that functions again this week. Here it is.
import matplotlib.pyplot as plt def plot_encoding(encodings, labels, sdr_width, num_features=None, title=""): colors = {'0': "red", '1': "blue", '2': "green"} plt.figure(figsize=(15,1)) # max(1, len(encodings)/10))) for idx, encoding in enumerate(encodings): label = labels[idx] xvals = [] yvals = [] for value in encoding: yvals.append(idx) xvals.append(value) plt.scatter(xvals, yvals, color=colors[label], marker='o') if num_features is not None: f_width = int(sdr_width / num_features) xpos = 0 while xpos <= sdr_width: plt.plot([xpos, xpos], [-1, len(encodings)+1], color="grey", linestyle="dotted") xpos += f_width plt.yticks(list(range(len(encodings)))) plt.ylim(-1, len(encodings)+1) plt.xlim(0, sdr_width) plt.title(title) plt.show()
Now let's create an encoder.
# encode the data by creating an encoder, configuring it, and then performing the encoding on train/test from niml.encoder import encoder nf = len(niml_data[0]) - 1 # get the number of features in the dataset my_encoder = encoder.Encoder(set_bits=5, sparsity=.5, field_types= ["N"] *nf, # all features are numeric cyclic_flags=[False]*nf, # none of the fields are cyclic spans= [ 0] *nf, # use simple/basic encoding bit-patterns cat_overlaps=[ 0] *nf, # N/A as data is numeric, not categorical. Set all features to 0 cat_values= [None] *nf, # N/A as data is numeric, not categorical. Set all features to None ) my_encoder.config_encoder(input_data=niml_data, label_col=0)
And now (for reference) we will encode a line of data from the wine dataset that has values for all features - nothing missing.
line_to_encode = niml_data[0] print("Data being encoded:\n ", line_to_encode) labels, encodings, sdr_width = my_encoder.encode(input_data=[line_to_encode], label_col=0) plot_encoding(encodings, labels, sdr_width, num_features=nf)
Data being encoded:
['2', 12.53, 5.51, 2.64, 25.0, 96.0, 1.79, 0.6, 0.63, 1.1, 5.0, 0.82, 1.69, 515.0]

Now - let's take that same line of data, and remove some of the values. We will replace them with the string "?" and we will tell the NIML system that a "?" is the character string that means "a value is missing"
After removing two features, let's encode this same line of data again and see the result.
import copy my_encoder.null_value = "?" # <------------- This line tell the encoder what a MISSING VALUE looks like missing_values_line = copy.deepcopy(niml_data[0]) missing_values_line[3] = "?" # replace the 3rd feature with a "missing value" missing_values_line[9] = "?" # replace the 9th feature with a "missing value" print("Data being encoded:\n ", missing_values_line) labels, encodings, sdr_width = my_encoder.encode(input_data=[missing_values_line], label_col=0) plot_encoding(encodings, labels, sdr_width, num_features=nf)
Data being encoded:
['2', 12.53, 5.51, '?', 25.0, 96.0, 1.79, 0.6, 0.63, '?', 5.0, 0.82, 1.69, 515.0]

The two graphs above show what happens when NIML comes across a missing value in the dataset. The NIML encoder simply skips over that field. No encoding is generated for that feature. When this encoding is passed into the NIML model, the model processes the input without any regard to the fact that some of the encoding bits are absent.
The important concept to observe is that the NIML system has a sematic way to represent "there is no value here". This is a unique property not found in other systems. Rather than having to replace a missing value with some placeholder, the NIML system allows for missing values to have their own unique representation.
There is one unavoidable impact of missing values on the NIML system. When a missing-value observation is encoded and passed to the pooler component, the pooler has no "signal" to latch onto at those missing-value positions. So during the reinforcement portion of the algorithm, the reinforcement can only be performed at positions where values are present. The result would be the convergenge of the pooler (the learning) at some positions might slightly outpace the convergence at other positions.
Note - imputation is not evil!
I want to take a brief pause to point out here that data imputation is NOT necessarily a bad practice. To the contraray, it is incredibly useful - it has allowed machine learning to progress. And the NIML system is completely capable of taking in a data file that has gone through imputation to fill in missing values. In fact, an imputed data file may perform BETTER in the NIML system than the same data file with missing values.
But data imputation is a whole process unto itself and can be a challenge. The benefit of the NIML system is that data impuation is not a required step. You can send your missing-values data through NIML and see how the results look. Then you can decide whether or not data imputation would be helpful.
Step 2 - Baseline (no missing values)As a second step in this challenge, let's just establish a baseline for the wine dataset when there are no missing features. We will create an encoder and a model, go through the learning process, and then evaluate the trained system.
# The base encoder - the one used above had parameters optimized for showing the
# "missing values" encoding.
my_encoder = encoder.Encoder(set_bits=15, sparsity=.1,
field_types= ["N"]*nf, # all features are numeric
cyclic_flags=[False]*nf, # none of the fields are cyclic
spans=[0]*nf, # use simple/basic encoding bit-patterns
cat_overlaps=[0]*nf, # N/A as data is numeric, not categorical. Set all features to 0
cat_values=[None]*nf, # N/A as data is numeric, not categorical. Set all features to None
missing_val_ind = "?",
)
my_encoder.config_encoder(input_data=niml_data, label_col=0)
from niml.model import model
sdr_width = my_encoder.sdr_width # default sdr width for any newly created model
def get_new_model(seed_val=97543, sw=sdr_width):
num_neurons = 3000
new_model = model.Model(
# Endoded Data parameters
sdr_width=sw, # Recieved from encoding the data
sdr_set_bits=12,
# NPU
neurons=num_neurons,
active_neurons=80,
input_pct=0.75,
learning=True,
synapse_inc=15,
synapse_dec=3,
# Boosting
boost_frequency=6,
boost_strength=0.09,
boost_bend_factor=0.175,
boost_table_length=21,
# Classifier
subclass_thresh=0.75,
min_overlap=0.0,
seed=seed_val,
)
return new_model
%%capture import time calc_times = [] results = [] random.seed(12345) for x in range(4): pooler_seed = random.randint(1,1000000) row_res = [] for y in range(4): tt_seed = random.randint(1,1000000) train, test = train_test_split(niml_data, test_size=0.28, random_state=tt_seed) train_labels, train_isdrs, sdr_width = my_encoder.encode(input_data=train, label_col=0) test_labels, test_isdrs, sdr_width = my_encoder.encode(input_data=test, label_col=0) start = time.time() my_model = get_new_model(pooler_seed) my_model.fit(labels=train_labels, isdrs=train_isdrs, epochs=9) res = my_model.evaluate(labels=test_labels, isdrs=test_isdrs) end = time.time() calc_times.append(end-start) row_res.append(res["accuracy_score"]) results.append(row_res)
print(sum(calc_times)) for row in results: print(row)
446.6265585422516 [0.98, 1.0, 0.98, 0.92] [0.98, 0.96, 1.0, 0.96] [0.98, 0.96, 1.0, 1.0] [1.0, 1.0, 1.0, 0.96]
1 epoch [0.84, 0.88, 0.9][0.86, 0.92, 0.88] [0.9, 0.9, 0.9]
2 epochs [0.9, 1.0, 0.92][0.96, 0.96, 0.92] [0.92, 0.88, 0.92]
3 epochs [0.9, 0.96, 0.96][0.94, 0.96, 0.94] [0.94, 0.94, 0.94]
4 epochs [0.9, 0.98, 0.96][0.96, 0.94, 0.94] [0.94, 0.94, 0.98]
5 epochs [0.94, 0.98, 0.94][0.92, 0.98, 0.96] [0.98, 0.94, 0.96]
new params 64.68244791030884 [0.98, 1.0, 0.98, 0.94][0.94, 1.0, 0.94, 0.98] [1.0, 0.94, 1.0, 1.0][1.0, 1.0, 0.98, 0.98]
6 epochs
7 epochs [0.94, 0.98, 0.96][0.96, 0.98, 0.94] [0.94, 0.96, 0.96] 90.60695052146912 [0.98, 1.0, 0.96, 0.94][0.94, 1.0, 0.98, 0.94] [0.98, 0.96, 0.98, 0.96][0.94, 1.0, 1.0, 0.98]
This seems like a decent place. Let's move on from here.
Step 3 - Missing data at InferenceLet's consider the scenario where a model has been very carefully constructed and is now running in a production environment. The model was constructed using a dataset that has NO missing values.
Out in production though, the data being presented to the system is not clean. Some observations have missing values for certain features. Can the system still make good predictions under these conditions?
Creating missing values
A small subroutine that will replace some of the true values in the dataset with missing values To be used on both our train dataset and on our test dataset
import copy def inject_missing_values(pct, dataset): # Make a copy of the dataset, overwrite PCT percentage of the values with "?" int_dataset = copy.deepcopy(dataset) num_rows = len(int_dataset) num_cols = len(int_dataset[0]) - 1 # Assumes labels are in column 0 total_values = num_rows * num_cols num_missing = int(pct * total_values) all_positions = list(range(total_values)) random.shuffle(all_positions) missing_ones = all_positions[:num_missing] for pos in sorted(missing_ones): row = int(pos / num_cols) col = pos % num_cols int_dataset[row][col+1] = "?" # again, assumes labels are in column 0 return int_dataset
To demonstrate how this function works
- let's first print out the original dataset (first 10 observations).
- generate a missing-values dataset with 30% missing values
- print out the missing-values dataset (first 10 observations)
The result is that 30% of the values are picked, at random, and those are converted into "?" as if the value were missing.
print("Original dataset:") for idx, row in enumerate(test[:10]): print(" observation #", idx, row) pm = 0.3 print("-"*50) test_missing = inject_missing_values(pm, test) print("Dataset with %0.02f missing values:" % pm) for idx, row in enumerate(test_missing[:10]): print(" observation #", idx, row)
Original dataset:
observation # 0 ['0', 13.05, 1.77, 2.1, 17.0, 107.0, 3.0, 3.0, 0.28, 2.03, 5.04, 0.88, 3.35, 885.0]
observation # 1 ['0', 12.93, 3.8, 2.65, 18.6, 102.0, 2.41, 2.41, 0.25, 1.98, 4.5, 1.03, 3.52, 770.0]
observation # 2 ['2', 13.69, 3.26, 2.54, 20.0, 107.0, 1.83, 0.56, 0.5, 0.8, 5.88, 0.96, 1.82, 680.0]
observation # 3 ['0', 13.3, 1.72, 2.14, 17.0, 94.0, 2.4, 2.19, 0.27, 1.35, 3.95, 1.02, 2.77, 1285.0]
observation # 4 ['0', 13.24, 2.59, 2.87, 21.0, 118.0, 2.8, 2.69, 0.39, 1.82, 4.32, 1.04, 2.93, 735.0]
observation # 5 ['2', 12.79, 2.67, 2.48, 22.0, 112.0, 1.48, 1.36, 0.24, 1.26, 10.8, 0.48, 1.47, 480.0]
observation # 6 ['1', 11.65, 1.67, 2.62, 26.0, 88.0, 1.92, 1.61, 0.4, 1.34, 2.6, 1.36, 3.21, 562.0]
observation # 7 ['0', 13.73, 1.5, 2.7, 22.5, 101.0, 3.0, 3.25, 0.29, 2.38, 5.7, 1.19, 2.71, 1285.0]
observation # 8 ['0', 14.06, 2.15, 2.61, 17.6, 121.0, 2.6, 2.51, 0.31, 1.25, 5.05, 1.06, 3.58, 1295.0]
observation # 9 ['1', 11.79, 2.13, 2.78, 28.5, 92.0, 2.13, 2.24, 0.58, 1.76, 3.0, 0.97, 2.44, 466.0]
--------------------------------------------------
Dataset with 0.30 missing values:
observation # 0 ['0', '?', 1.77, 2.1, 17.0, '?', '?', 3.0, 0.28, 2.03, 5.04, '?', 3.35, 885.0]
observation # 1 ['0', 12.93, 3.8, 2.65, 18.6, 102.0, 2.41, 2.41, 0.25, '?', 4.5, 1.03, 3.52, 770.0]
observation # 2 ['2', 13.69, 3.26, '?', 20.0, 107.0, 1.83, '?', '?', 0.8, 5.88, '?', 1.82, 680.0]
observation # 3 ['0', 13.3, 1.72, 2.14, 17.0, '?', '?', '?', 0.27, 1.35, 3.95, 1.02, 2.77, 1285.0]
observation # 4 ['0', '?', 2.59, '?', 21.0, 118.0, '?', 2.69, '?', 1.82, '?', 1.04, 2.93, 735.0]
observation # 5 ['2', 12.79, '?', 2.48, 22.0, 112.0, '?', 1.36, 0.24, 1.26, '?', '?', 1.47, 480.0]
observation # 6 ['1', '?', 1.67, 2.62, 26.0, 88.0, 1.92, '?', '?', '?', 2.6, '?', 3.21, 562.0]
observation # 7 ['0', 13.73, 1.5, 2.7, '?', '?', 3.0, 3.25, 0.29, 2.38, 5.7, 1.19, 2.71, 1285.0]
observation # 8 ['0', 14.06, 2.15, 2.61, '?', 121.0, 2.6, 2.51, 0.31, 1.25, 5.05, '?', 3.58, '?']
observation # 9 ['1', 11.79, 2.13, '?', 28.5, '?', 2.13, 2.24, 0.58, '?', '?', 0.97, 2.44, '?']
Now lets take the baseline model created above, and run a missing-values dataset through it. In fact, we will run multiple missing-values datasets through with different settings for how much data is missing at each step. We will then plot the accuracy of the system as it makes predictions against a set of missing-values observations.
run_results = [] random.seed(34335) for run in range(8): pct_missing = [] accuracy = [] for p5mark in range(21): pm = 0.05*p5mark test_missing = inject_missing_values(pm, test) pct_missing.append(pm) test_labels, test_isdrs, sdr_width = my_encoder.encode(input_data=test_missing, label_col=0) res = my_model.evaluate(labels=test_labels, isdrs=test_isdrs) accuracy.append(res["accuracy_score"]) run_results.append( (pct_missing, accuracy) ) #print(accuracy)
import matplotlib.pyplot as plt plt.figure(figsize=(20,8)) for x in run_results: pct_missing = x[0] accuracy = x[1] plt.plot(pct_missing, accuracy) plt.scatter(pct_missing, accuracy) plt.title("INFERENCE: Percent Missing values vs. Accuracy") plt.xlabel('Percent missing values') plt.xticks([x/10 for x in list(range(11))]) plt.ylabel('Accuracy') plt.ylim(0.0,1.1) #plt.yticks([x/10 for x in list(range(11))]) plt.yticks([0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]) plt.grid() plt.show()

Step 4 - Missing data at Training
%%capture
#####################
# Note - this block can take ~10 minutes to complete
import time
my_encoder.null_value = "?"
results = []
run_num = 0
random.seed(6374)
start = time.time()
for pooler_loop in range(3):
pooler_seed = random.randint(1,1000000)
row_res = []
for tt_loop in range(2):
tt_seed = random.randint(1,1000000)
train, test = train_test_split(niml_data, test_size=0.28, random_state=tt_seed)
pooler_res = []
xvals = []
print("Starting run", run_num)
for p5mark in range(15):
print(" mark", p5mark)
pm = 0.05*p5mark
xvals.append(pm)
train = inject_missing_values(pm, train)
train_labels, train_isdrs, sdr_width = my_encoder.encode(input_data=train, label_col=0)
test_labels, test_isdrs, sdr_width = my_encoder.encode(input_data=test, label_col=0)
my_model = get_new_model(pooler_seed)
my_model.fit(labels=train_labels, isdrs=train_isdrs, epochs=8)
res = my_model.evaluate(labels=test_labels, isdrs=test_isdrs)
pooler_res.append(res["accuracy_score"])
print(pooler_res)
print(xvals)
results.append( (xvals, pooler_res) )
print("finished run", run_num)
run_num += 1
end = time.time()
print("Total time:", end-start)
Total time: 1114.729336977005
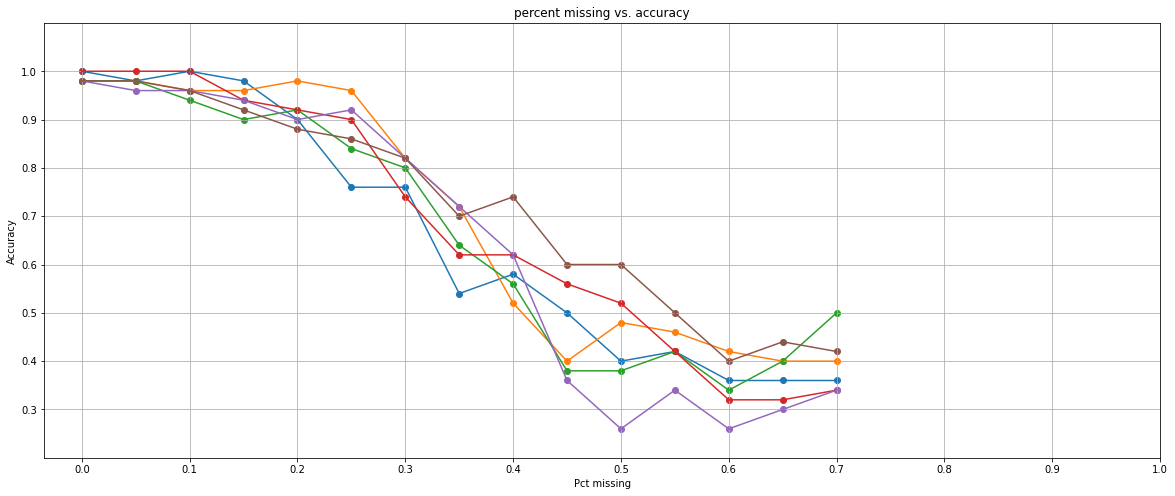
import matplotlib.pyplot as plt plt.figure(figsize=(20,8)) for x in results: pct_missing = x[0] accuracy = x[1] plt.plot(pct_missing, accuracy) plt.scatter(pct_missing, accuracy) plt.title("percent missing vs. accuracy") plt.xlabel('Pct missing') plt.xticks([x/10 for x in list(range(11))]) plt.ylabel('Accuracy') plt.ylim(0.2,1.1) plt.yticks([0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]) plt.grid() plt.show()
Yes - the seems to be a relationshp between the total number of neurons and the number of active neurons, at least for the dataset I explored here and within the context of the other hyperparameters at their current settings. It appears that for a given number of total neurons, we should have between 5% and 10% of them active to achieve the best accuracy.
It would be curious to explore this relationship within other datasets. And to explore this relationship and whether other hyperparameters affect this.
- Do more complex datasets require more neurons overall?
- Is there even a metric of difficulty for different datasets out there?
- Does the 5% to 10% rule-of-thumb seen here (ratio of active neurons to total neurons) hold across other datasets
- Does this ratio change if other hyperparameters change?
- What if the input_percent were higher or lower? Does a more-connected or less-connected neuron lead to a different ratio of active-to-total neurons in the system?
- How about number of epochs? Could that have an effect on this experiment?
